4-02. Sin(), Cos() & noise(+random)
4-01. point() & if()
4-02. Sin(), Cos() & noise(+random)
4-03. 거리에 대해
4-04. Clamp() -> fit() -> Chramp()
4-05. Copy to Point + 정보의 이동
addpoint 펑션 끼워팔기(?)
attribwrangle(run over : detail once)
vector pos = {2,0,0};
addpoint(0,pos);
for반복문
int k = int(@Frame);
for(int i=0 ; i < k ; i++){
addpoint(0,set(i,0,0));
}
. i<k : i가 k라는 변수보다 작을때 까지(k 변수 보다 커지면 멈춤)
. i++ : i는 1씩 커짐
. addpoint 펑션으로 점을 만들고 싶은데, i라는 값을 활용해서 만들고 싶다.
. int(@Frame); : @Frame는 float정보 type을 int로 변경
. int k = int(@Frame); : k값으로 프레임을 쓰겠다. - 시간이 진행됨에 따라 포인트가 만들어짐
int k = int(@Frame);
for(int i=0 ; i < k ; i++){
vector pos = set(chf("speed")*i,0,0);
addpoint(0,pos);
}
. add - by group : 선형
. chf("speed")* : 선이 만들어 지는 속도 (값0 이라서 파라미터 만들어 지지 않아 +켜주고 speed값 1)
1차 함수(리니어)
y = x
y = (x -1) + 2 / y=x+1
y = a(x - b) +c : a=1, b=2, c=4 -> x가 2이고 y가 4인 점을 지나는
기울기 1짜리 선이 만들어짐.
기울기 y=x -> a(기울기)가 2이면 y=2x 기울기

2차 함수(도자기형)
y = x제곱
y = (x-1)제곱 + 3
y = 2(x+2)제곱 - 2
y = a(x-b)제곱 + c : a=1, b=1, c=3 -> x가 1이고 y가 3인 중점을 지나는 보자기형 선
기울기가 가파르다/완만하다 = 리니어 선형 간격이 쪼그라들었다/늘어났다.

y = a(x - b)d제곱 + c
-> y = a x function(x - x_offeset) + y_offest
함수는 시각적으로 생각했을때
표준 모양이나 패턴을 어디에 둘 것인지
그 패턴의 폭을 어떠한 간격으로 확대 축소를 할 것인지.
funtion의 표준모양을 기준으로 위치로 바꾸는 건 offset
패턴의 사이즈와 폭은 곱해주는 값 a

run over : detail(only once)
1d(1차함수) : float Y = a*(X-b)+c;
2d(2차함수) : float Y = a*(X-b)*(X-b)+c;
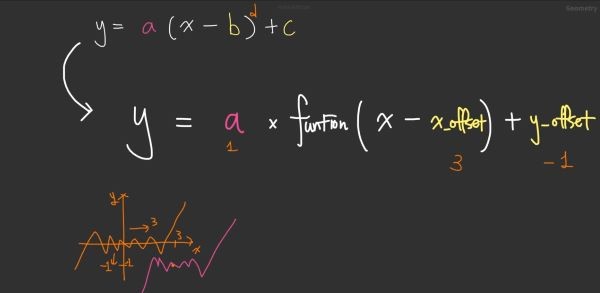
sin 펑션(점대칭)
y = a(x-b)+c;
-> y = a function(X - b) + c;
-> y = function(a *(X - b)) + c; : sin, con, noise에 올바로 작동하는 식
= sin(a *(X - b)) + c;
cos 펑션(좌우대칭)
float Y = cos(a *(X - b)) + c;
amp(높낮이)
float Y = amp * sin(a *(X - b)) + c;
noise
float Y = amp * noise(a *(X - b)) + c;
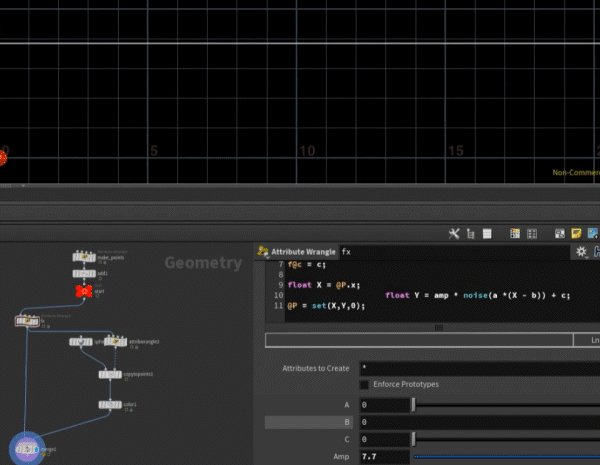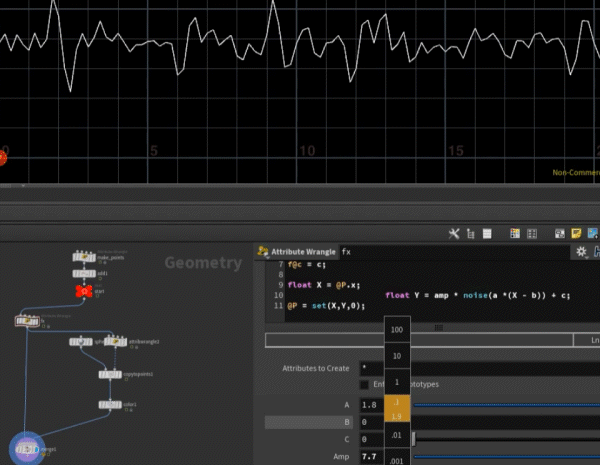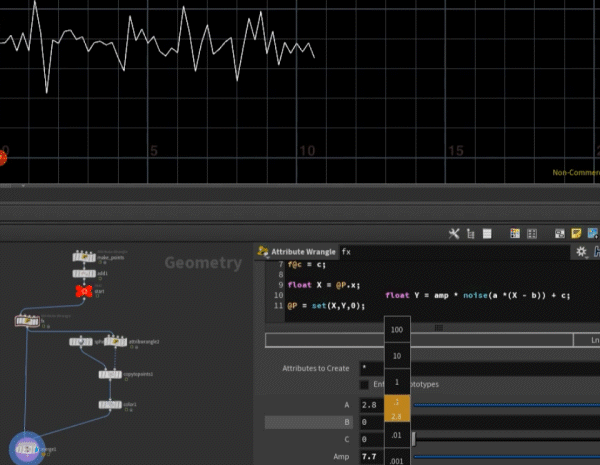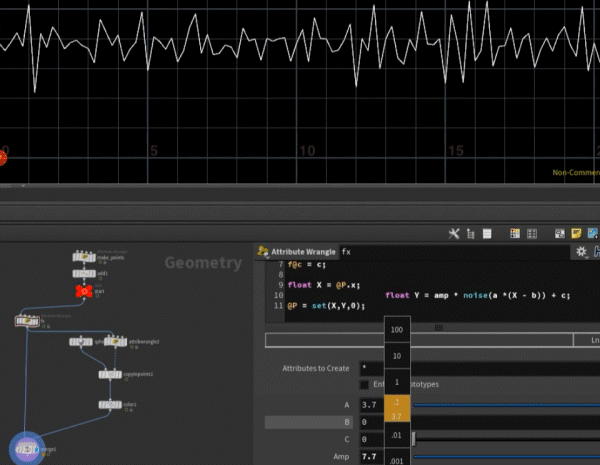
내 정신과 마음의 패턴인가 ㄷㄷㄷ
float 나 = 마음 * noise(정신*(X-시간)) + 회피 ??!?!?!?
오늘도 ㅠoㅠ
'공부 일기 > 후디니 입문' 카테고리의 다른 글
| [공부일기] 15일차 쳅터4 - 04. VEX Functions : Clamp() & Fit() (0) | 2024.02.06 |
|---|---|
| [공부일기] 12일차 챕터4 - 01. VEX Functions : Point() & 조건문 if (1) | 2024.02.06 |
| [공부일기] 11일차 챕터3 - 04. 시계 시스템 with VOP (1) | 2024.02.06 |
| [공부일기] 10일차 챕터3 - 03. 시계 시스템 with VEX, Point() 사진 (0) | 2024.02.06 |
| [공부일기] 9일차 쳅터3 - 02. 정보의 연산 & VOP 기초 (0) | 2024.02.06 |



